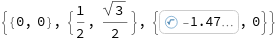Evaluate

Basic Examples

Using ϕ, the golden ratio or Fibonacci’s rabbit constant, convert points to the algebraic number field
(ϕ)
and build the Fermat triangle:

ϕ=GoldenRatio;​​points={{0,0},{0,1},{-Sqrt[ϕ],0}};​​Column
○
SqrtSpace
[ϕ,points],Graphics[{EdgeForm[Black],Yellow,Polygon[points]}]
In[]:=
{{{0,0},{0,0}},{{0,0},{1,0}},{{0,-1},{0,0}}}
Out[]=

Using ψ, the supergolden ratio or Narayana’s cow constant, convert points to the algebraic number field
(ψ)
and build the supergolden triangle:

ψ=Root-1-#1
2
+#1
3
&,1;​​points={0,0},
1
2
,
3
2
,{-ψ,0};​​Column
○
SqrtSpace
[ψ,points],Graphics[{EdgeForm[Black],Yellow,Polygon[points]}]
In[]:=
{{0,0,0},{0,0,0}},
1
4
,0,0,
3
4
,0,0,{{0,0,-1},{0,0,0}}
Out[]=

Convert back to the original points:

○
SqrtSpace
ψ,{{0,0,0},{0,0,0}},
1
4
,0,0,
3
4
,0,0,{{0,0,-1},{0,0,0}}
In[]:=
{0,0},
1
2
,
3
2
,,0
Out[]=

Properties and Relations

Under “Neat Examples” in ref/GeometricScene is a mysterious output after “Decompose a triangle into similar triangles”:

RandomInstance[GeometricScene[{a,b,c,d,g,e,f},{​​p0Polygon[{e,g,f}],​​p1Style[Polygon[{a,b,c}],Cyan],​​p2Style[Polygon[{b,c,d}],Purple],​​p3Style[Polygon[{d,c,g}],Red],​​p4Style[Polygon[{g,c,a}],Green],​​p5Style[Polygon[{e,d,b}],Blue],​​p6Style[Polygon[{g,a,f}],Magenta],​​GeometricAssertion[{p0,p1,p2,p3,p4,p5,p6},"Similar"],​​a=={-1/2,0},b=={1/2,0}}],RandomSeeding5]
In[]:=
Out[]=

This triangle is in the algebraic number field / geometric space of
(ρ)
where ρ is the plastic constant:

ρ=Root-1-#1+#1
3
&,1;vals=-
1
4
,0,0,{0,0,0},
1
4
,0,0,{0,0,0},0,
1
4
,
1
4
,-
1
4
,
3
4
,
1
4
,1,
5
4
,
5
4
,-
1
4
,
3
4
,
1
4
,
9
4
,4,3,{0,0,0},-
9
4
,-4,-3,{0,0,0},
1
4
,
1
4
,-
1
4
,1,
7
4
,
7
4
;triangles={{1,2,3},{2,3,4},{4,3,7},{7,3,1},{5,4,2},{7,1,6}};​​points=
○
SqrtSpace
[ρ,vals];​​Graphics[{EdgeForm[Black],{Hue[Area[#]],#}&/@(Polygon[points[[#]]]&/@triangles)}]
In[]:=
Out[]=

Convert the points back to original values:

○
SqrtSpace
[ρ,points]
In[]:=
-
1
4
,0,0,{0,0,0},
1
4
,0,0,{0,0,0},0,
1
4
,
1
4
,-
1
4
,
3
4
,
1
4
,1,
5
4
,
5
4
,-
1
4
,
3
4
,
1
4
,
9
4
,4,3,{0,0,0},-
9
4
,-4,-3,{0,0,0},
1
4
,
1
4
,-
1
4
,1,
7
4
,
7
4
Out[]=

A simple application of ToNumberField doesn’t recognize the points as being in either
(ρ)
or

ρ
, but does recognize the values when they get squared:

ρ=Root-1-#1+#1
3
&,1;​​Column​​Quiet@ToNumberField[points[[3]],ρ],​​Quiet@ToNumberFieldpoints[[3]],
ρ
,​​ToNumberField[points[[3]]^2,ρ]
In[]:=

These values are algebraic numbers:

The actual point is also a pair of algebraic number:

The signs here happen to be positive so taking the square root of the algebraic version doesn’t require extra steps:

Neat Examples

Plot out the points: