Basic Examples

Plot a spirograph:

○
Spirograph
5
∑
j=1

jφ
j+1
,φ
In[]:=
Out[]=

A more complicated spirograph:

○
Spirograph
13
∑
j=1
Cosj
2

jφ
,φ
In[]:=
Out[]=

Half of the path of the spirograph:

○
Spirograph
13
∑
j=1
Cosj
2

jφ
,φ,π
In[]:=
Out[]=

Convert the curve to a polygon:

○
Spirograph
13
∑
j=1
Cosj
2

jφ
,φ/.LinePolygon
In[]:=

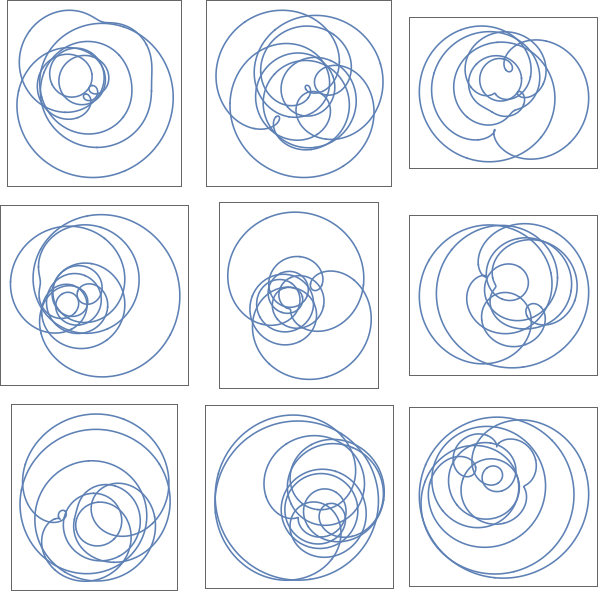
A spirograph with random values:

Options

ColorFunction

Choose a ColorFunction:

"MaurerPolygons"

Set explicit values for “MaurerPolygons”:

Default values for “MaurerPolygons”:

"ShowCircles"

Show the ‘wheels’ that generate the spirograph:

Make an animation:

Applications

Spirographs had an important application in the 1940s, when they were used for the "manual" solution of polynomial equations of higher degree. To understand this, let us consider the following polynomial poly in the variable z:

We show the spirographs for a range of values of r:

Let us zoom to a neighborhood of the origin:

Here is an even closer look:

These are absolute values and arguments of the zeros of the polynomial:

The spirograph curves corresponding to these absolute values all go through the origin: