TriangularSpiralPoints | Example Notebook

Basic Examples
(4)

Here are the points on the first four legs of the spiral:

In[96]:=

[◼]	TriangularSpiralPoints

[4]

Out[96]=

{0,0},-

1

2

,

3

2

,{-1,0},-

3

2

,-

3

2

,-

1

2

,-

3

2

,

1

2

,-

3

2

,

3

2

,-

3

2

,{1,0},

1

2

,

3

2

,0,

3

,-

1

2

,

3

2



———

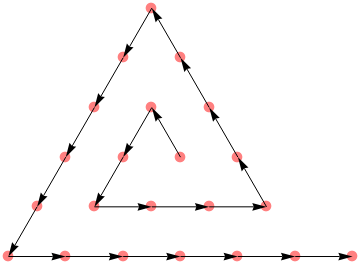
This shows the sequence of points in order for the first six sides:

In[97]:=

Withs=

[◼]	TriangularSpiralPoints

[6],Graphics[{{Pink,PointSize[.03],Point[s]},Arrow@Partition[s,2,1]}]

Out[97]=

———

40 black sides with 20 red sides overlaid:

In[98]:=

GraphicsLine@

[◼]	TriangularSpiralPoints

[40],Red,Line@

[◼]	TriangularSpiralPoints

[20]

Out[98]=

———

The number of points in the first

n

sides are one more than the triangular numbers:

In[67]:=

Length@

[◼]	TriangularSpiralPoints

@#&/@Range[0,10]

Out[67]=

{1,2,4,7,11,16,22,29,37,46,56}

In[68]:=

Table[1+1/2n(n+1),{n,0,10}]

Out[68]=

{1,2,4,7,11,16,22,29,37,46,56}

Basic Examples (4)

Neat Examples (2) 

Basic Examples
(4)

Neat Examples
(2)

