Basic Examples

Sample evolution of a symbolic system:

○
SymbolicSystem
[{e[x_][y_]x[e[y]][x]},e[e[e][e]][e][e],5]//Column
In[]:=
e[e[e][e]][e][e]
e[e][e][e[e]][e[e][e]][e]
e[e[e]][e][e[e]][e[e[e]][e]][e]
e[e][e[e]][e[e]][e[e]][e[e][e[e]][e[e]]][e]
e[e[e[e]]][e][e[e]][e[e]][e[e[e[e]]][e][e[e]]][e]
e[e[e]][e[e]][e[e[e]]][e[e]][e[e]][e[e[e]][e[e]][e[e[e]]][e[e]]][e]
Out[]=

Define the auxiliary function
ToBrackets
:

ToBrackets[rule_,init_,steps_]:=Module{e},​​StringSplit[StringReplace[ToString[#1],"e"->""],""]&/@
○
SymbolicSystem
[rule,init,steps];
In[]:=
ToBrackets[e[x_][y_]x[e[y]][x],e[e[e][e]][e][e],5]//Column
In[]:=
{[,[,],[,],],[,],[,]}
{[,],[,],[,[,],],[,[,],[,],],[,]}
{[,[,],],[,],[,[,],],[,[,[,],],[,],],[,]}
{[,],[,[,],],[,[,],],[,[,],],[,[,],[,[,],],[,[,],],],[,]}
{[,[,[,],],],[,],[,[,],],[,[,],],[,[,[,[,],],],[,],[,[,],],],[,]}
{[,[,],],[,[,],],[,[,[,],],],[,[,],],[,[,],],[,[,[,],],[,[,],],[,[,[,],],],[,[,],],],[,]}
Out[]=

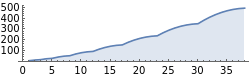
Steps versus step lengths:

ListLinePlotLength/@ToBrackets[e[x_][y_]x[e[y]][x],e[e[e][e]][e][e],37],FillingAxis,AspectRatio
1
4
In[]:=
Out[]=

Plot the evolution of the symbolic system:

Module{evolved=ToBrackets[e[x_][y_]x[e[y]][x],e[e[e][e]][e][e],5]},GraphicsFlattenTableBlack,EdgeForm[Thin],evolved〚j〛〚i〛/.{"]"White,"["
,Rectangle[{i-1,1-j},{i,2-j}],evolved〚j〛〚i〛/.{"]"
,"["
,TextStyleevolved〚j〛〚i〛,FontSize8,
1
2
(2i-1),
1
2
(3-2j),{j,Length[evolved]},i,Lengthevolved〚j〛
In[]:=
Out[]=
Module[{evolved=ToBrackets[e[x_][y_]x[e[y]][x],e[e[e][e]][e][e],37]},ArrayPlot[evolved/.{"]"0,"["1},PixelConstrained5,ColorRules{0LightGray,1Black},FrameFalse]]
In[]:=
Out[]=