Basic Examples

Generate a sequence of random reals and apply a discrete cosine transform-based test:
sequence=RandomReal[{0,1},1000];
In[]:=
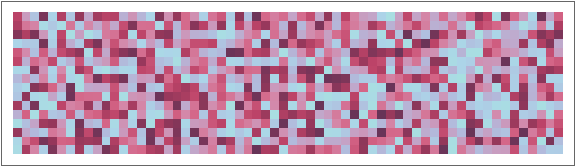
Visualize the sequence:
ArrayPlotPartition[sequence,16],

In[]:=
Out[]=
[◼]
SpectralRandomnessTest
[sequence,"TestStatistic"]
In[]:=
0.0186997
Out[]=
[◼]
SpectralRandomnessTest
[sequence,"PValue"]
In[]:=
0.559604
Out[]=
Generate a sequence of random integers and apply a discrete cosine transform-based test:
sequence=RandomInteger[{0,1},1000];
In[]:=
Visualize the sequence:
ArrayPlotPartition[sequence,16],

In[]:=
Out[]=
[◼]
SpectralRandomnessTest
[sequence,"TestStatistic"]
In[]:=
0.0129432
Out[]=
[◼]
SpectralRandomnessTest
[sequence,"PValue"]
In[]:=
0.967207
Out[]=

Scope

Attempt to reject a non-random sequence:
subsequence=RandomInteger[{0,1},100];
In[]:=
sequence=Flatten[Table[subsequence,20]];
In[]:=
ArrayPlotPartition[Take[sequence,200],25],

In[]:=
Out[]=
[◼]
SpectralRandomnessTest
[sequence,"TestStatistic"]
In[]:=
KolmogorovSmirnovTest
:Ties exist in the data and will be ignored for the KolmogorovSmirnov test, which assumes unique values.
0.298392
Out[]=
[◼]
SpectralRandomnessTest
[sequence,"PValue"]
In[]:=
KolmogorovSmirnovTest
:Ties exist in the data and will be ignored for the KolmogorovSmirnov test, which assumes unique values.
0.
Out[]=

Applications

Test to see if rule 30 is random according to the spectral test:
rule30seq=CellularAutomaton[30,{{1},0},{10000,0}]〚1〛;
In[]:=
ArrayPlotPartition[Take[rule30seq,100],25],

In[]:=
Out[]=
[◼]
SpectralRandomnessTest
[rule30seq]
In[]:=
0.226717
Out[]=

Possible Issues

For non-random data, the Kolmogorov–Smirnov test, a part of the entire test, may return ties. Observing such ties is a strong indicator that the data is non–random:

Neat Examples

Visualize the sampling distribution of the test statistic: