Basic Examples (3)
Basic Examples
(3)
Maximize the second value:
In[1]:=
Out[1]=
{{{1,3,2},{2,3,1}},3}
———
Given a function that takes a permutation of the numbers , determine the maximum function value:
{1,2,3}
In[1]:=
f[{1,2,3}]=2;f[{1,3,2}]=9;f[{2,1,3}]=1;f[{2,3,1}]=-3;f[{3,1,2}]=9;f[{3,2,1}]=5;
The result shows that there are two permutations, and , that both yield the maximal value :
{1,3,2}
{3,1,2}
f=9
In[2]:=
Out[2]=
{{{1,3,2},{3,1,2}},9}
———
Construct a function that takes a permutation of the numbers and whose global maximum is known:
{1,2,…,100}
In[1]:=
m=100;x=RandomReal[{0,1},m];g=#.x&;
The global maximum of is given by the permutation that is in the same numerical order as the list :
g
x
In[2]:=
g[Ordering[Ordering[x]]]
Out[2]=
3495.21
Find the maximum of by a Monte Carlo search though the space of possible permutations:
g
m!≈9×
157
10
In[3]:=
5
10
Out[3]=
{{{91,90,84,44,5,37,11,25,92,47,94,95,39,82,7,46,15,71,54,63,69,41,79,56,78,22,67,8,26,42,100,23,76,59,75,10,74,68,96,73,61,55,6,35,65,14,85,27,60,64,53,40,19,33,62,28,52,66,38,3,18,9,24,21,49,1,77,50,87,12,99,45,83,43,86,2,70,29,97,72,36,58,98,13,89,34,80,17,31,57,16,81,20,32,88,48,51,4,30,93}},3492.9}
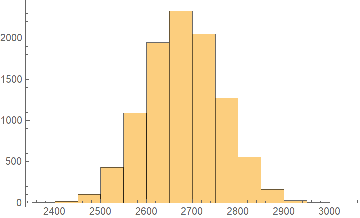
This result is not quite optimal, but close. It is much larger than the typical values of found by applying random permutations directly:
g
In[4]:=
Histogram[Table[g[RandomSample[Range[m]]],]]
4
10
Out[4]=
Scope (1)
Scope
(1)
Applications (8)
Applications
(8)