Basic Examples (6)
Basic Examples
(6)
Compute the points of discontinuity of a rational function:
In[9]:=
Out[9]=
{{x-4}}
Repeat the calculation, classifying the points of discontinuity:
In[10]:=
Out[10]=
{{x-4,TypeInfinite discontinuity,LeftLimit∞,ValueAtDiscontinuityComplexInfinity,RightLimit-∞}}
———
Compute the points of discontinuity of a trigonometric function:
In[11]:=
Out[11]=
∈&&xπ+
1
1
2
1
Repeat the calculation, classifying the points of discontinuity:
In[12]:=
Out[12]=
∈&&xπ+,TypeInfinite discontinuity,LeftLimit∞,ValueAtDiscontinuityComplexInfinity,RightLimit-∞
1
1
2
1
———
Compute the points of discontinuity of a smooth function:
In[15]:=
Out[15]=
{}
———
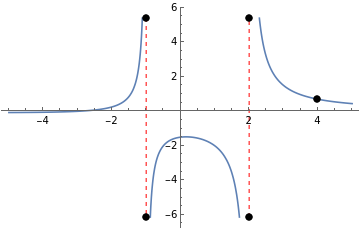
Compute and plot the points of discontinuity of a rational function:
In[13]:=
f[x_]:=(-12-x+)/(8+2x-5+);[f[x],x,"Properties"]
2
x
2
x
3
x
Out[14]=
{x-1,TypeInfinite discontinuity,LeftLimit∞,ValueAtDiscontinuityComplexInfinity,RightLimit-∞},{x2,TypeInfinite discontinuity,LeftLimit-∞,ValueAtDiscontinuityComplexInfinity,RightLimit∞},x4,TypeRemovable discontinuity,LeftLimit,ValueAtDiscontinuityIndeterminate,RightLimit
7
10
7
10
In[16]:=
Plot[f[x],{x,-5,5},ExclusionsStyle{{Red,Dashed},{PointSize0.02}}]
Out[16]=
———
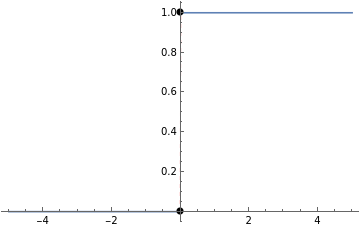
Compute and plot the points of discontinuity of a step function:
In[17]:=
f[x_]:=HeavisideTheta[x];[f[x],x,"Properties"]
Out[18]=
{{x0,TypeJump discontinuity,LeftLimit0,ValueAtDiscontinuityHeavisideTheta[0],RightLimit1}}
In[3]:=
Plot[f[x],{x,-5,5},ExclusionsStyle{{Red,Dashed},{PointSize0.02}}]
Out[3]=
———
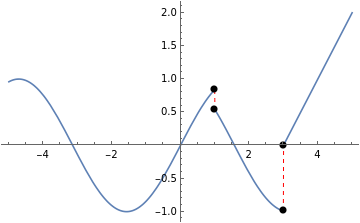
Compute and plot the points of discontinuity of a step function:
In[19]:=
f[x_]:=Piecewise[{{Sin[x],x<1},{Cos[x],x>1&&x<3}},x-3];[f[x],x,"Properties"]
Out[20]=
{{x1,TypeJump discontinuity,LeftLimitSin[1],ValueAtDiscontinuity-2,RightLimitCos[1]},{x3,TypeJump discontinuity,LeftLimitCos[3],ValueAtDiscontinuity0,RightLimit0}}
In[3]:=
Plot[f[x],{x,-5,5},ExclusionsStyle{{Red,Dashed},{PointSize0.02}}]
Out[3]=
———
Options (1)
Options
(1)
Properties and Relations (1)
Properties and Relations
(1)
Possible Issues (1)
Possible Issues
(1)